WPP#2: Unit A Concept 7: Profit, Revenue, and Cost

WPP#1: Unit A Concept 6: Writing and Solving Linear Models

SV#5: Unit J Concepts 3-4: Solving Three-Variable Systems with Gaussian Elimination

The viewer needs to pay special attention to the four steps of the Gaussian Elimination. Make sure you have plugged in the system correctly into your matrix. Look over your adding/subtracting, make sure it is done correctly so no simple mistakes are made. At the end where you find each value, make sure that you check on your calculator using rref to make sure your answers are correct. Always double check to make sure each step was done correctly and followed the steps to the Gaussian Elimination.

Fibonacci Haiku: Batman

Batman
Gotham
Arkham's worst
Rule by fear
Keep control or lose it
Batman is the only solution. Batman will win.

SP #5 Unit J Concept 6: Partial Fraction Decomposition with Repeated Factors

This concept deals with repeated factors to you must count up the powers. Set up the factors in A,B,C, etc. letters. Towards the end use the calculator in RREF to get the answer to do back substitution to check your answer is right.

SP #4 Unit J Concept 5: Partial Fraction Decomposition with Distinct Factors

Pay spacial attention for any mistakes. Make sure to separate the denominators with letters (A,B,C, etc). Multiply each denominator with what its missing and group all the like terms. At the end make sure to put A,B,C, etc. back to its corresponding fractions from the beginning.

SP#2: Unit E Concept 7: Graphing polynomials, including: x-int, zeroes (with multiplicities), end behavior. All polynomials will be factorable.

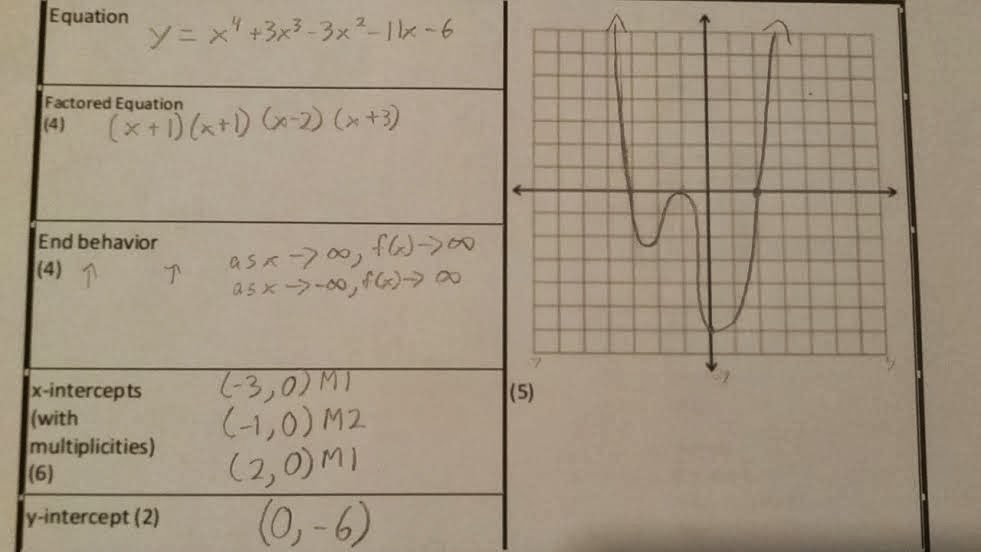 In concept 7, you'll be able to do a full evaluation of factorable polynomials and describe every aspect. The aspects are how the extremes behave, how the middle behaves, where the highest and lowest points are, where the intercepts are, and what intervals they are (increasing or decreasing).

     Pay attention in the multiplicity of zeros because its a big deal. if the multiplicity is 1 the graph goes through or if its 2 the graph bounces or if its 3 the graph curves. Each multiplicity represents a gate, so the graph can't go through unless there's a gate. To find the extremes you must use the graphing calculator using second calc.

SP#1: Unit E Concept 1: Identifying x-intercepts, y-intercepts, vertex (max/min), axis of quadratics and graphing them. Quadratics in standard form

This concept will more into detail for graphing quadratics.in unit B, you only graph the quadratic using the shifts of the parent function. now you'll go a step further to make the graph more accurate and detailed by identifying the vertex, x and y-intercepts, and the axis of symmetry.
     Pay attention to start in standard form (f(x)=ax^2+bx+c) then complete the square to put the parent function form in f(x)=a(x-h)^2+k. The graph will include 2 to 4 points, those points will be the vertex, the x and y-intercepts, and the axis. To get the vertex its the (h,k) of the parent function, h will always be the opposite ex. h=2 it will be -2 for the vertex.

WPP #4: Unit E Concept 3

Create your own Playlist on MentorMob!

WPP #3 Unit E Concept 2

Create your own Playlist on MentorMob!

SV #2 Unit G Concepts 1-7 Graphing functions

SV #3 Unit H Concept 7: Finding logs given approximations

SP #3 Unit I Concept 1: Graphing Exponential Functions

In this concept you will be learning how to graph exponential functions as well as identify the x-intercepts, y-intercepts, asymptotes, domain and range. The parent graph is y = a times b^(x-h) + k. You will be using the parent graph to find the asymptote, the x-intercepts, y-intercepts, domain and range.

Be careful plugging 0 into y to find the x-intercept as well as plugging in 0 for x when finding the y intercept. Make sure that you are using your algebra solving skills correctly when finding the intercepts. Remember that you CANNOT take the log or natural log of a negative number (if is undefined and that means that you will not have a x intercept). Remember to put arrows on the ends of your graph because it goes on forever.

Problem: f(x) = 3(2^x-5)+4

WPP #6 Unit I Concepts 3-5 - Investment Application Problem

Create your own Playlist on MentorMob!