Fibonacci Haiku: Batman

Batman
Gotham
Arkham's worst
Rule by fear
Keep control or lose it
Batman is the only solution. Batman will win.

SP #5 Unit J Concept 6: Partial Fraction Decomposition with Repeated Factors

This concept deals with repeated factors to you must count up the powers. Set up the factors in A,B,C, etc. letters. Towards the end use the calculator in RREF to get the answer to do back substitution to check your answer is right.

SP #4 Unit J Concept 5: Partial Fraction Decomposition with Distinct Factors

Pay spacial attention for any mistakes. Make sure to separate the denominators with letters (A,B,C, etc). Multiply each denominator with what its missing and group all the like terms. At the end make sure to put A,B,C, etc. back to its corresponding fractions from the beginning.

SP#2: Unit E Concept 7: Graphing polynomials, including: x-int, zeroes (with multiplicities), end behavior. All polynomials will be factorable.

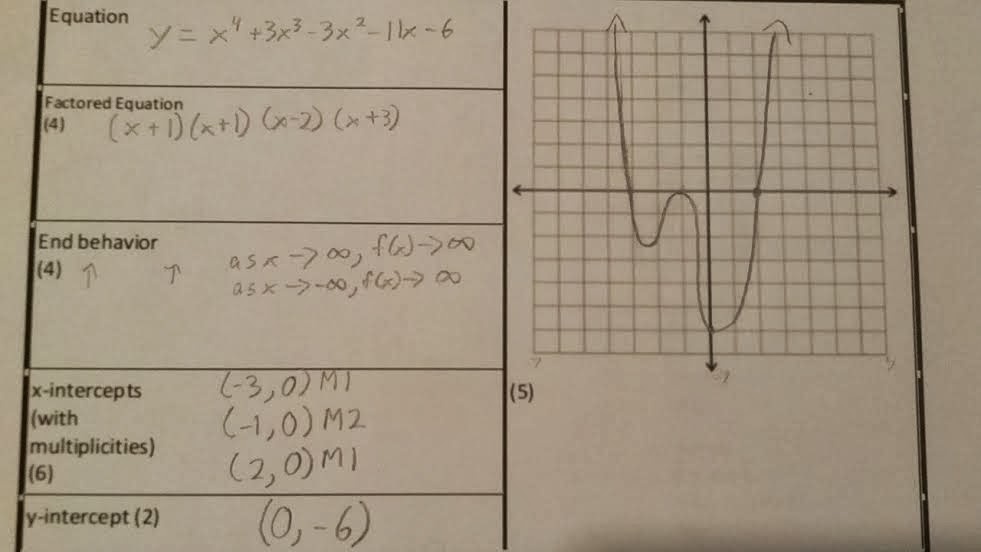 In concept 7, you'll be able to do a full evaluation of factorable polynomials and describe every aspect. The aspects are how the extremes behave, how the middle behaves, where the highest and lowest points are, where the intercepts are, and what intervals they are (increasing or decreasing).

     Pay attention in the multiplicity of zeros because its a big deal. if the multiplicity is 1 the graph goes through or if its 2 the graph bounces or if its 3 the graph curves. Each multiplicity represents a gate, so the graph can't go through unless there's a gate. To find the extremes you must use the graphing calculator using second calc.

SP#1: Unit E Concept 1: Identifying x-intercepts, y-intercepts, vertex (max/min), axis of quadratics and graphing them. Quadratics in standard form

This concept will more into detail for graphing quadratics.in unit B, you only graph the quadratic using the shifts of the parent function. now you'll go a step further to make the graph more accurate and detailed by identifying the vertex, x and y-intercepts, and the axis of symmetry.
     Pay attention to start in standard form (f(x)=ax^2+bx+c) then complete the square to put the parent function form in f(x)=a(x-h)^2+k. The graph will include 2 to 4 points, those points will be the vertex, the x and y-intercepts, and the axis. To get the vertex its the (h,k) of the parent function, h will always be the opposite ex. h=2 it will be -2 for the vertex.

WPP #4: Unit E Concept 3

Create your own Playlist on MentorMob!

WPP #3 Unit E Concept 2

Create your own Playlist on MentorMob!

SV #2 Unit G Concepts 1-7 Graphing functions

SV #3 Unit H Concept 7: Finding logs given approximations